John Kerl Graduate student Department of Mathematics University of Arizona http://math.arizona.edu/~kerl E-mail: kerl at math dot arizona dot edu

My research centers on Markov chain Monte Carlo methods in statistical mechanics. This includes side work on lattice percolation and self-avoiding walks. My thesis topic is critical behavior for the model of random spatial permutations. This project lies at the crossroads of probability theory, statistical mechanics, functional analysis, statistics, and numerical methods.

The random-spatial-permutation model arises in the study of the Bose gas, although it is also of intrinsic probabilistic interest; its history includes Bose-Einstein, Feynman, Penrose-Onsager, Sütő, and Ueltschi-Betz. Random permutations arise physically when one symmetrizes the N-boson Hamiltonian with pair interactions and applies a multi-particle Feynman-Kac formula. System energy is now expressed in terms of point positions and permutations of positions, where permutations occur with non-uniform probability. Feynman’s claim is that BEC occurs if and only if there are infinite cycles. The central point of this approach is that the system energy has been recast in terms of permutations, which are amenable to analysis and simulation. Furthermore, interactions between permutations are recast as collision probabilities between Brownian bridges in Feynman time. These Brownian bridges are integrated out, resulting in a model which lends itself readily to simulations without the need for CPU-intensive path-integral Monte Carlo (PIMC). This permits a new perspective on the venerable question: how does the critical temperature of Bose-Einstein condensation depend on inter-particle interaction strength?

Obtaining a full answer to this question is a long-term project. Breaking it into manageable pieces, my co-advisor Daniel Ueltschi and I consider modified Hamiltonians as well as various point configurations. For example, points may distributed throughout the continuum or held fixed on a lattice. Through careful use of MCMC algorithms, statistical analysis, and finite-size scaling, we are able to quantify the dependence of critical temperature on interaction strength for certain models.

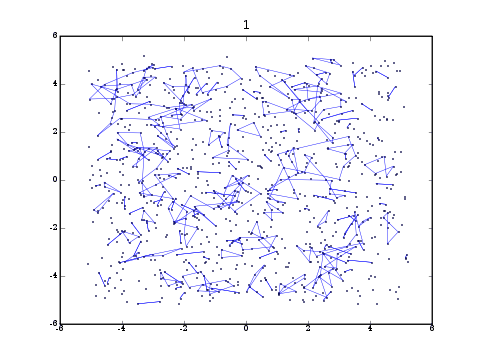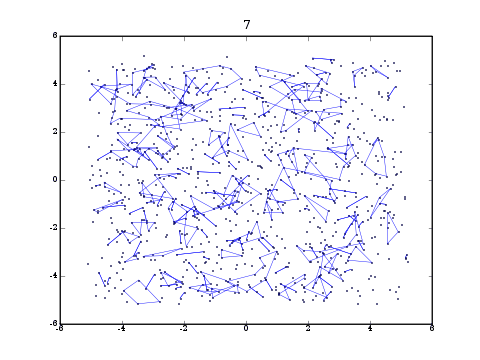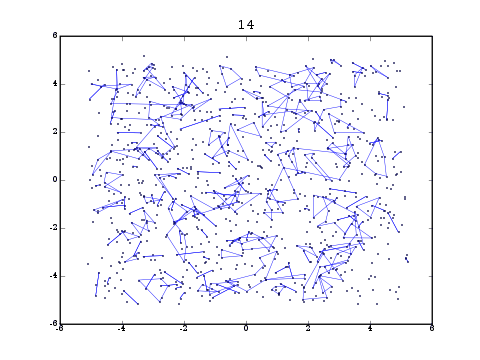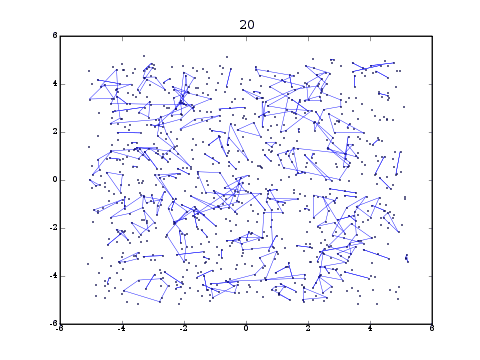
In the animation at the top of this page, there are 10³ points uniformly distributed in a 3-dimensional box. There are no interactions and the temperature is sub-critical. Lines between points indicate permutation cycles. Twenty permutations are displayed.

For more information, please click here.